

The slope of two lines must be equal in order for them to be parallel.


On a 2D plane, the distance of two parallel lines can be calculated by finding the perpendicular distance between the lines.Distance between two lines is referred to as the shortest distance of parallel lines that can be cut from one point to another.Such a situation is possible only in 3-dimensions or more. The term Skew lines refer to the lines that exist in the multidimensional system, where two lines are non-parallel but never intersect with each other. Read More: Construction of Parallel Lines from an External Point Also if the equations of the parallel lines are given in the form ax + by + c1 = 0 and ax + by + c2 = 0 Here, c1 is the constant of line l1 and c2 is the constant for line l2, and m represents the slope of the line. The formula for distance between two parallel lines having the slope-intercept form of equations of the two lines as y = mx + c1 and y = mx + c2 And it does not matter which perpendicular line we are choosing, as long as two points are on the line.īecause of this, we can now easily calculate the distance between two parallel lines and the distance between a point and a line. We have previously discussed that the shortest distance between the two parallel lines can be determined using the length of the perpendicular segment between the lines. Read More: X and Y Intercepts, Form, Graph and Formula The formula for the distance if the equations of the parallel lines are given in the ax +by +c1 = 0 and ax +by +c2 = 0, is as follows: Also, in this case, m represents the slope of the line. In the above formula, c1 is the constant of line l1 and c2 is the constant for line l2. The formula for the distance if we have the slope-intercept form of the two lines as y = mx + c1 and y = mx + c2 is: Read More: Different Forms of the Equation of Lineīelow given is the formula for distance between two parallel lines. Finally, we put all the values in the distance formula discussed below to find the distance between two lines.Replace the previous values in the slope-intercept equation to calculate the value of y.
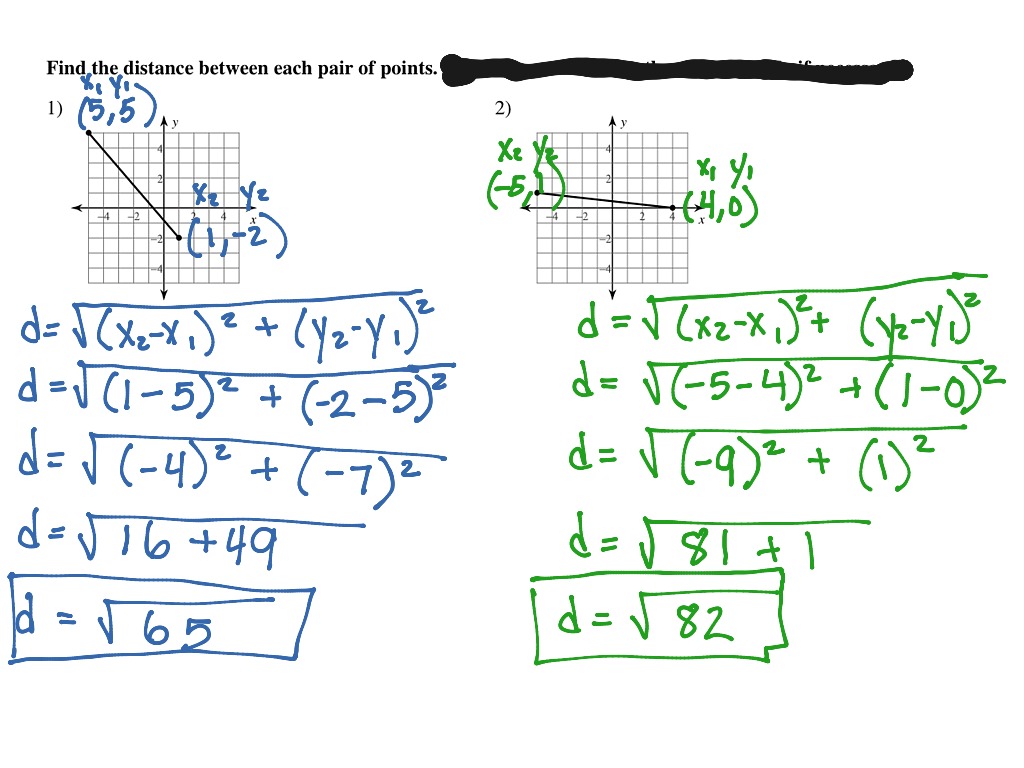
After that, we find the value of the interception point (c1 and c2) and find the value of the slope for both the lines.The slope value should be common for both lines if the equations of lines are given in the slope-intercept form.In order to calculate the distance, we check whether the given equations of parallel lines are in slope-intercept form (i.e.The steps to calculate the distance between two lines are as follows: Steps to Calculate Distance Between Two Lines For skew lines, the distance between two skew lines is equal to the length of the perpendicular between the lines.For intersecting lines, the shortest distance between both the lines is eventually zero.For parallel lines, the distance between two parallel lines is the perpendicular distance from any point on one line to the other line.We come across various different sets of lines such as parallel lines, intersecting lines, or skew lines. The minimum distance between any two points lying on the lines is basically the distance between two straight lines. The distance between two lines can be measured with the help of the two points that are there on each of the lines.


 0 kommentar(er)
0 kommentar(er)
